Приведенная система вычетов. Модульная арифметика Приведенная система по модулю 9

Согласно свойству сравнений №15, числа одного и того же класса по модулю m имеют с модулем m один и тот же НОД. Особенно важны классы, для которых он равен 1.

Взяв от каждого из таких классов по одному числу, получим приведенную систему вычетов по модулю m . Обычно ее выделяют из системы наименьших неотрицательных вычетов по модулю m .

Приведенная система наименьших неотрицательных вычетов по модулю m обозначается U m .

Количество чисел в приведенной системе вычетов по модулю m , очевидно, равно φ(m ).

Пример :

Приведенная система вычетов по модулю 15 есть {1; 2; 4; 7; 8; 11; 13; 14}. Заметим, что φ(15)=(5–1)∙(3–1)= 8 и действительно, в приведенной системе вычетов по модулю 15 ровно 8 элементов.

Утверждение 1

Любые φ(m ) чисел, попарно несравнимых по модулю m и взаимно простых с m , образуют приведенную систему вычетов.

(Доказательство очевидно как в утверждении 1 пункт 2)

Утверждение 2

Если (a , m ) = 1, x пробегает приведенную систему вычетов по модулю m , то ax тоже пробегает приведенную систему вычетов по модулю m . (Доказательство очевидно как в утверждении 2 пункт 2).

Обратный элемент.

Говорят, что элемент b называется обратным к a по модулю m , если a∙b ≡1(mod m ), и пишут b ≡ a –1 (mod m ).

Вообще, классическая теория чисел не нуждается в таком понятии как обратный элемент, в чем можно убедиться, ознакомившись, например, с . Однако криптология использует системы вычетов как в теоретико-числовом, так и в алгебраическом аспекте, а потому, для удобства изложения алгебраических основ криптологии, мы вводим понятие обратного элемента.

Возникает вопрос – для всех ли элементов по данному модулю m существует обратный (по умножению), и если для каких-то элементов обратный существует, как его найти?

Для ответа на этот вопрос воспользуемся расширенным алгоритмом Евклида. Рассмотрим сначала взаимно простые число a и модуль m . Тогда, очевидно, (a ,m )=1. Расширенный алгоритм Евклида позволяет получить числа x и y , такие, что ax+my= (a ,m ), или, что то же самое, ax+my =1. Из последнего выражения получаем сравнение ax+my ≡1(mod m ). Поскольку my ≡0(mod m ), то ax ≡1(mod m ), а значит полученное с помощью расширенного алгоритма Евклида число x как раз и есть искомый обратный элемент к числу a по модулю m .

Пример.

a =5, m =7. Требуется найти a -1 mod m .

Воспользуемся расширенным алгоритмом Евклида.

Обратный ход:

1=5–2∙2=5–(7–5∙1)∙2=5∙3–7∙2.

x =3, y =–2.

5 -1 ≡3(mod 7)

Проверка: 5∙3=15. 15≡1(mod 7).

Действительно, 3 является обратным элементом к 5 по модулю 7.

Итак, конструктивным образом убедились в том, что для чисел, взаимно простых с модулем, существует обратный по этому модулю. А существуют ли обратные элементы для чисел, не являющихся с модулем взаимно простыми?

Пусть (a ,m )=d ≠1. Тогда a и m представимы в виде a =d ∙a 1 , m =d ∙m 1 . Допустим, что для a существует обратный элемент по модулю m, то есть b : a ∙b ≡1(modm ). Тогда a ∙b= m ∙k +1. Или, что то же самое, d ∙a 1 ∙b= d ∙m 1 ∙k +1. Но тогда по теореме 2 из §1 п.1, в силу того, что и левая часть данного уравнения, и первое слагаемое в правой части делятся на d , то d \1, а это не так, поскольку d ≠1. Пришли к противоречию, следовательно предположение о существовании обратного элемента неверно.

Итак, мы только что доказали

Теорему обратимости

a -1 (mod m ) (a , m ) = 1.

Суммируя все рассуждения этого пункта, можем сказать, что обратимыми являются только взаимно простые с модулем числа, и найти обратные для них можно с помощью расширенного алгоритма Евклида.

Совокупность чисел, сравнимых с a по модулю m называется классом чисел по модулю m (или классом эквивалентности). Все числа одного класса имеют вид mt + r при фиксированном r .

При заданном m , r может принимать значения от 0 до m -1, т.е. всего существует m классов чисел по модулю m , и любое целое число попадет в один из классов по модулю m . Таким образом,

Z = m m … [m -1] m , где [r ] m ={x Z: x ≡r (mod m )}

Любое число класса [r ] m называется вычетом по модулю m по отношению ко всем числам того же класса. Число, равное остатку r , называется наименьшим неотрицательным вычетом .

Вычет, наименьший по абсолютной величине, называется абсолютно наименьшим вычетом .

Пример

Возьмем модуль m =5. И пусть a =8. Разделим a на m с остатком:

Остаток r =3. Значит 8 5 , и наименьший неотрицательный вычет числа 8 по модулю 5 есть 3.

Абсолютно наименьший вычет можно отыскать, вычислив r-m=3-5=-2, и сравнив абсолютные величины |-2| и |3|. |-2|<|3|, значит -2 – абсолютно наименьший вычет числа 8 по модулю 5.

Взяв от каждого класса по одному вычету, получим полную систему вычетов по модулю m . Если все эти числа будут являться наименьшими неотрицательными вычетами по модулю m , то такая система вычетов называется полной системой наименьших неотрицательных вычетов , и обозначается Z m .

{0; 1;…; m -1} = Z m – полная система наименьших неотрицательных вычетов.

{– ;…; 0;…; } (если m –нечетное число) ;

{ - ,…,-1, 0, 1,…, } или {- ,…, -1, 0, 1,…, } (если m четное число) – полная система абсолютно наименьших вычетов.

Пример

Если m =11, то полная система наименьших неотрицательных вычетов есть {0; 1; 2; 3; 4; 5; 6; 7; 8; 9; 10}, а полная система абсолютно наименьших вычетов – {–5; –4; –3; –2; –1; 0; 1; 2; 3; 4; 5}.

Утверждение 1

Любые m чисел, попарно несравнимые по модулю m , образуют полную систему вычетов по этому модулю.

Доказательство:

Действительно, в силу несравнимости эти числа принадлежат к разным классам, а т.к. их m штук, то в каждый существующий класс попадает ровно одно число.

Утверждение 2

Если (a , m ) = 1, и x пробегает полную систему вычетов по модулю m , то ax +b , где b – любое число из Z, тоже пробегает полную систему вычетов по модулю m .

Доказательство:

Чисел ax +b будет ровно m штук. Остается доказать, что любые 2 числа ax 1 +b и ax 2 +b несравнимы по модулю m , если x 1 x 2 (mod m )

Доказательство от противного. Предположим, что ax 1 +b ≡ ax 2 +b (mod m ) в силу 4-го св-ва сравнений, ax 1 ≡ ax 2 (mod m ) в силу св-ва сравнений №9 и того, что (a , m ) = 1, имеем x 1 ≡ x 2 (mod m ). Получили противоречие с тем, что x 1 x 2 (mod m ). Следовательно, предположение неверно, а значит верно обратное. То есть ax 1 +b и ax 2 +b несравнимы по модулю m , если x 1 x 2 (mod m ), что и требовалось доказать.

Пункт 17. Полная и приведенная системы вычетов.

В предыдущем пункте было отмечено, что отношение є m сравнимости по произвольному модулю m есть отношение эквивалентности на множестве целых чисел. Это отношение эквивалентности индуцирует разбиение множества целых чисел на классы эквивалентных между собой элементов, т.е. в один класс объединяются числа, дающие при делении на m одинаковые остатки. Число классов эквивалентности є m (знатоки скажут - "индекс эквивалентности є m ") в точности равно m .

Определение. Любое число из класса эквивалентности є m будем называть вычетом по модулю m . Совокупность вычетов, взятых по одному из каждого класса эквивалентности є m , называется полной системой вычетов по модулю m (в полной системе вычетов, таким образом, всего m штук чисел). Непосредственно сами остатки при делении на m называются наименьшими неотрицательными вычетами и, конечно, образуют полную систему вычетов по модулю m . Вычет r называется абсолютно наименьшим, если пrп наименьший среди модулей вычетов данного класса.

Пример : Пусть m = 5 . Тогда:

0, 1, 2, 3, 4 - наименьшие неотрицательные вычеты;

2, -1, 0, 1, 2 - абсолютно наименьшие вычеты.

Обе приведенные совокупности чисел образуют полные системы вычетов по модулю 5 .

Лемма 1. 1) Любые m штук попарно не сравнимых по модулю m чисел образуют полную систему вычетов по модулю m .

2) Если а и m взаимно просты, а x m , то значения линейной формы аx+b , где b - любое целое число, тоже пробегают полную систему вычетов по модулю m .

Доказательство. Утверждение 1) – очевидно. Докажем утверждение 2). Чисел аx+b ровно m штук. Покажем, что они между собой не сравнимы по модулю m . Ну пусть для некоторых различных x 1 и x 2 из полной системы вычетов оказалось, что ax 1 +b є ax 2 +b(mod m) . Тогда, по свойствам сравнений из предыдущего пункта, получаем:

ax 1 є ax 2 (mod m)

x 1 є x 2 (mod m)

– противоречие с тем, что x 1 и x 2 различны и взяты из полной системы вычетов.

Поскольку все числа из данного класса эквивалентности є получаются из одного числа данного класса прибавлением числа, кратного m , то все числа из данного класса имеют с модулем m один и тот же наибольший общий делитель. По некоторым соображениям, повышенный интерес представляют те вычеты, которые имеют с модулем m наибольший общий делитель, равный единице, т.е. вычеты, которые взаимно просты с модулем.

Определение. Приведенной системой вычетов по модулю m называется совокупность всех вычетов из полной системы, взаимно простых с модулем m .

Приведенную систему обычно выбирают из наименьших неотрицательных вычетов. Ясно, что приведенная система вычетов по модулю m содержит j ( m ) штук вычетов, где j ( m )– функция Эйлера – число чисел, меньших m и взаимно простых с m . Если к этому моменту вы уже забыли функцию Эйлера, загляните в пункт 14 и убедитесь, что про нее там кое-что говорилось.

Пример. Пусть m = 42. Тогда приведенная система вычетов суть:

1, 5, 11, 13, 17, 19, 23, 25, 29, 31, 37, 41.

Лемма 2. 1) Любые j ( m ) чисел, попарно не сравнимые по модулю m и взаимно простые с модулем, образуют приведенную систему вычетов по модулю m .

2) Если (a,m) = 1 и x пробегает приведенную систему вычетов по модулю m , то аx так же пробегает приведенную систему вычетов по модулю m .

Доказательство. Утверждение 1) – очевидно. Докажем утверждение 2). Числа аx попарно несравнимы (это доказывается так же, как в лемме 1 этого пункта), их ровно j ( m ) штук. Ясно также, что все они взаимно просты с модулем, ибо (a,m)=1, (x,m)=1 Ю (ax.m)=1 . Значит, числа аx образуют приведенную систему вычетов.

Таковы определения и основные свойства полной и приведенной систем вычетов, однако в багаже математических знаний существует еще целый ряд очень интересных и полезных фактов, касающихся систем вычетов. Если умолчать про них в этом пункте, то это, боюсь, будет прямым нарушением Закона Российской Федерации об Информации, злонамеренное утаивание которой является, согласно этому закону, административно и, даже, уголовно наказуемым деянием. Кроме того, без знакомства с дальнейшими важными свойствами систем вычетов пункт 17 получится весьма куцым. Продолжим.

Лемма 3. Пусть m 1 , m 2 , ..., m k – попарно взаимно просты и m 1 m 2 ...m k =M 1 m 1 =M 2 m 2 =...=M k m k , где

1) Если x 1 , x 2 , ..., x k пробегают полные системы вычетов по модулям m 1 , m 2 , ..., m k пробегают полную систему вычетов по модулю m=m 1 m 2 ...m k .

2) Если x 1 , x 2 , ..., x k пробегают приведенные системы вычетов по модулям m 1 , m 2 , ..., m k соответственно, то значения линейной формы пробегают приведенную систему вычетов по модулю m=m 1 m 2 ...m k .

Доказательство.

1) Форма M 1 x 1 +M 2 x 2 + ...+M k x k принимает, очевидно, m 1 m 2 ...m k =m значений. Покажем, что эти значения попарно несравнимы. Ну пусть

M 1 x 1 +M 2 x 2 + ...+M k x k є M 1 x 1 С +M 2 x 2 С + ...+M k x k С (mod m)

Всякое M j , отличное от M s , кратно m s . Убирая слева и справа в последнем сравнении слагаемые, кратные m s , получим:

M s x s є M s x s С (mod m s) Ю x s є x s С (mod m s)

– противоречие с тем, что x s пробегает полную систему вычетов по модулю m s .

2). Форма M 1 x 1 +M 2 x 2 + ...+M k x k принимает, очевидно, j ( m 1 ) j ( m 2 ) Ч ... Ч j ( m k ) = j ( m 1 m 2 Ч ... Ч m k )= j ( m ) (функция Эйлера мультипликативна!) различных значений, которые между собой по модулю m=m 1 m 2 ...m k попарно несравнимы. Последнее легко доказывается рассуждениями, аналогичными рассуждениям, проведенным при доказательстве утверждения 1) этой леммы. Так как ( M 1 x 1 +M 2 x 2 + ...+M k x k ,m s)=(M s x s ,m s)=1 для каждого 1 Ј s Ј k , то ( M 1 x 1 +M 2 x 2 + ...+M k x k ,m s)=1 , следовательно множество значений формы M 1 x 1 +M 2 x 2 + ...+M k x k образует приведенную систему вычетов по модулю m .

Лемма 4. Пусть x 1 , x 2 , ..., x k ,x пробегают полные, а x 1 , x 2 ,..., x k , x – пробегают приведенные системы вычетов по модулям m 1 , m 2 , ..., m k и m=m 1 m 2 ...m k соответственно, где (m i m j)=1 при i № j . Тогда дроби совпадают с дробями {x/m} , а дроби совпадают с дробями { x /m} .

Доказательство. Доказательство обоих утверждений леммы 4 легко получается применением предыдущей леммы 3 после того, как вы приведете каждую сумму {x 1 /m 1 +x 2 /m 2 +...+x k /m k } и { x 1 /m 1 + x 2 /m 2 +...+ x k /m k } к общему знаменателю:

{x 1 /m 1 +x 2 /m 2 +...+x k /m k }={(M 1 x 1 +M 2 x 2 +...+M k x k)/m} ;

{ x 1 /m 1 + x 2 /m 2 +...+ x k /m k }={(M 1 x 1 +M 2 x 2 +...+M k x k)/m} ,

где M j =m 1 ...m j-1 m j+1 ...m k .

Если теперь принять во внимание, что дробные части чисел, получающихся при делении на модуль m любых двух чисел, сравнимых по модулю m , одинаковы (они равны r/m , где r – наименьший неотрицательный вычет из данного класса), то утверждения настоящей леммы становятся очевидными.

В оставшейся части этого пункта произойдет самое интересное – мы будем суммировать комплексные корни m -ой степени из единицы, при этом нам откроются поразительные связи между суммами корней, системами вычетов и уже знакомой мультипликативной функцией Мебиуса m ( m ) .

Обозначим через e k k -ый корень m- ой степени из единицы:

Эти формы записи комплексных чисел мы хорошо помним с первого курса. Здесь k=0,1,...,m-1 – пробегает полную систему вычетов по модулю m .

Напомню, что сумма e 0 + e 1 +...+ e m-1 всех корней m -ой степени из единицы равна нулю для любого m . Действительно, пусть e 0 + e 1 +...+ e m-1 =a . Умножим эту сумму на ненулевое число e 1 . Такое умножение геометрически в комплексной плоскости означает поворот правильного m -угольника, в вершинах которого расположены корни e 0 , e 1 ,..., e m-1 , на ненулевой угол 2 p /m . Ясно, что при этом корень e 0 перейдет в корень e 1 , корень e 1 перейдет в корень e 2 , и т.д., а корень e m-1 перейдет в корень e 0 , т.е. сумма e 0 + e 1 +...+ e m-1 не изменится. Имеем e 1 a=a , откуда a=0 .

Теорема 1. Пусть m>0 - целое число, a О Z , x пробегает полную систему вычетов по модулю m . Тогда, если а кратно m , то

в противном случае, при а не кратном m ,

.

Доказательство. При а кратном m имеем: a=md и

При а не делящемся на m , разделим числитель и знаменатель дроби a/m на d – наибольший общий делитель а и m , получим несократимую дробь a 1 /m 1 . Тогда, по лемме 1, a 1 x будет пробегать полную систему вычетов по модулю m . Имеем:

ибо сумма всех корней степени m 1 из единицы равна нулю.

Напомню, что корень e k m -ой степени из единицы называется первообразным, если его индекс k взаимно прост с m . В этом случае, как доказывалось на первом курсе, последовательные степени e k 1 , e k 2 ,..., e k m-1 корня e k образуют всю совокупность корней m -ой степени из единицы или, другими словами, e k является порождающим элементом циклической группы всех корней m -ой степени из единицы.

Очевидно, что число различных первообразных корней m -ой степени из единицы равно j ( m ), где j – функция Эйлера, так как индексы у первообразных корней образуют приведенную систему вычетов по модулю m .

Теорема 2. Пусть m>0 – целое число, x пробегает приведенную систему вычетов по модулю m . Тогда (сумма первообразных корней степени m ):

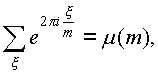
где m ( m ) – функция Мебиуса.

Доказательство. Пусть m=p 1 a 1 p 2 a 2 ...p k a k – каноническое разложение числа m ; m 1 =p 1 a 1 , m 2 =p 2 a 2 , m 3 =p 3 a 3 ; x i пробегает приведенную систему вычетов по модулю m i . Имеем:

При a s =1 получается, что только корень e 0 =1 не является первообразным, поэтому сумма всех первообразных корней есть сумма всех корней минус единица:

стало быть, если m свободно от квадратов (т.е. не делится на r 2 , при r >1 ), то

Если же какой-нибудь показатель a s больше единицы (т.е. m делится на r 2 , при r>1 ), то сумма всех первообразных корней степени m s есть сумма всех корней степени m s минус сумма всех не первообразных корней, т.е. всех корней некоторой степени, меньшей m s . Именно, если m s =p s m s * , то:

Вот теперь, дорогие читатели, когда я представил на ваше рассмотрение довольно весьма значительное количество сведений про полные и приведенные системы вычетов, никто не сможет обвинить меня в злонамеренном нарушении Закона Российской Федерации об Информации посредством ее утаивания, поэтому я заканчиваю этот пункт с удовлетворением.

Определение. Числа образуют полную систему вычетов по модулю , если любое целое число сравнимо по модулю с одним и только одним из этих чисел.

Любая полная система вычетов по модулю состоит из чисел, которые попарно не сравнимы по модулю .

Теорема. Пусть - полная система вычетов по модулю . Пусть - целое число, взаимно простое с . Тогда - тоже полная система вычетов по модулю .

Доказательство. Нужно доказать, что эти числа попарно не сравнимы по модулю . Предположим противное. Пусть

Так как НОД , то , что противоречит условию.

Теорема. Пусть - полная система вычетов по модулю . Пусть - целое число. Тогда - тоже полная система вычетов по модулю .

Лемма. Если , то НОД НОД .

Доказательство.

– целое число.

Отсюда . Любой общий делитель и является делителем . Отсюда НОД НОД .

Определение. Числа образуют приведенную систему вычетов по модулю , если они взаимно просты с и любое целое число, взаимно простое с , сравнимо с одним и только одним из этих чисел по модулю .

Пример. Приведенная система вычетов по модулю 10: 1,3,7,9.

Лемма. Все приведенные системы вычетов по модулю состоят из одного и того же количества чисел, которое обозначается - функция Эйлера.

Доказательство. Действительно, пусть есть две приведенные системы вычетов по модулю , состоящие из разного количества чисел:

Тогда так как числа образуют приведенную систему вычетов по модулю , то каждое из чисел сравнимо с одним и только одним из этих чисел. Поскольку , то, по принципу Дирихле, по крайней мере два числа из будут сравнимы с каким-то числом , а значит, будут сравнимы между собой по модулю . А это противоречит тому, что - приведенная система вычетов по модулю . Значит, .

Докажем теперь, что . В самом деле, числа, меньшие и взаимно простые с , образуют приведенную систему вычетов по модулю . Это следует из леммы.

Определение. Функция Эйлера (или тотиент) обозначает количество чисел, меньших и взаимно простых с .

Теорема. Если - приведенная система вычетов по модулю и - число, взаимно простое с , то - тоже приведенная система вычетов по модулю .

Если - простое, то .

Лемма. Если - простое, то .

Доказательство. Действительно, чисел, меньших простого и имеющих с ним общий делитель, всего .

Лемма. Пусть НОД . Тогда . Функция Эйлера мультипликативна.

Доказательство. Запишем все числа от 1 до следующим образом:

Числа в каждой строке образуют полную систему вычетов по модулю . Значит, взаимно простых с среди них . При этом эти числа расположены по столбцам - друг под другом, поскольку в каждом столбце стоят числа, сравнимые по модулю .

Числа в каждом столбце образуют полную систему вычетов по модулю . Действительно, -й столбец получается, если взять числа , образующие полную систему вычетов по модулю , умножить их на число , взаимно простое с , и прибавить к каждому из них .

Таким образом, в каждом столбце ровно чисел, взаимно простых с .

Так как число будет взаимно простым с тогда и только тогда, когда оно взаимно просто с и взаимно просто с , то количество чисел, взаимно простых с , равно .

Теорема. Пусть

Каноническое разложение числа . Тогда

Доказательство. По лемме о мультипликативности функции Эйлера

Пример.

Теорема (Эйлера). Если и - взаимно простые числа, то

Пусть - какая-нибудь приведенная система вычетов по модулю . . Тогда - тоже приведенная система вычетов по модулю . Следовательно, каждое из чисел первой последовательности сравнимо с одним из чисел второй последовательности по модулю , а каждое из чисел второй последовательности сравнимо с одним из чисел первой последовательности. Тогда

Так как каждое из чисел взаимно просто с , то на них сравнение можно сократить:

Следствие. Пусть – целые числа, – натуральные. Если , , НОД , то .

Доказательство. Пусть . Так как , то – натуральное число. Тогда

Значит, .

88вопрос
Гомотетия и подобие пространства

Гомотетию с центром O и коэффициентом k обозначают H k 0

Свойства преобразований гомотетии и подобия пространства аналогичны свойствам гомотетии и подобия плоскости, поэтому изучение первых следует начинать с повторения вторых. Подобие пространства с коэффициентом k можно разложить в композицию движения и гомотетии с некоторым центром и тем же коэффициентом.

Учащиеся должны знать, что при подобном преобразовании пространства сохраняется величина угла (плоского и двугранного), параллельные (перпендикулярные) прямые и плоскости отображаются на параллельные (перпендикулярные) прямые и плоскости. Это означает, что при подобном преобразовании пространства образом любой фигуры является фигура, имеющая такую же форму, что и данная фигура, но отличающаяся от нее лишь «своими размерами».

Задача 12. Дан правильный тетраэдр РАВС ; точки Р 1 , А 1 , В 1 , С 1 - центры его граней (рис.14). Докажите, что тетраэдр Р 1 А 1 В 1 С 1 подобен тетраэдру РАВС ; найдите коэффициент этого подобия.

Решение . Пусть точки Н и K - середины ребер соответственно АВ и ВС тетраэдра РАВС , точка А 1 - центр грани РВС , точка Р 1 - центр грани АВС (рис. 14). Это означает, что

РА 1: А 1 K = АР 1: Р 1 K = 2: 1,

А 1 K : РK = Р 1 K : АK = 1: 3,

Аналогично можно доказать, что
А 1 В 1 : АВ = 1: 3 и А 1 В 1 АВ ,
А 1 С 1 : АС = 1: 3 и А 1 С 1 АС ,
В 1 С 1 : ВС = 1: 3 и В 1 С 1 ВС ,
В 1 Р 1 : ВР = 1: 3 и В 1 Р 1 ВР ,
С 1 Р 1 : СР = 1: 3 и С 1 Р 1 СР .
Из этих соотношений между ребрами тетраэдров РАВС и Р 1 А 1 В 1 С 1 следует, что тетраэдр Р 1 А 1 В 1 С 1 - правильный, поэтому эти тетраэдры подобны; коэффициент подобия равен 1/3. (В профильных классах стоит доказать, что эти тетраэдры гомотетичны.)
Можно ввести определение: «Фигура F 1 называется подобной фигуре F , если существует преобразование подобия пространства, отображающее фигуру F на фигуру F 1 ». Тогда для доказательства подобия фигуры F 1 фигуре F достаточно найти хотя бы одно преобразование подобия, которое фигуру F отображает на фигуру F 1 ..

Определение. Параллельным переносом, или, короче, переносом фигуры, называется такое ее отображение, при котором все ее точки смещаются в одном и том же направлении на равные расстояния, т.е. при переносе каждым двум точкам X и Y фигуры сопоставляются такие точки X" и Y", что XX" = YY"

Основное свойство переноса:

Параллельный перенос сохраняет расстояния и направления, т.е. X"Y" = XY

Отсюда выходит, что параллельный перенос есть движение, сохраняющее направление и наоборот, движение, сохраняющее направление, есть параллельный перенос

Из этих утверждений также вытекает, что композиция параллельных переносов есть параллельный перенос

Параллельный перенос фигуры задается указанием одной пары соответствующих точек. Например, если указано, в какую точку A" переходит данная точка A, то этот перенос задан вектором AA", и это означает, что все точки смещаются на один и тот же вектор, т.е. XX" = AA" для всех точек Х

Центральная симметрия

Определение

Точки A и A" называются симметричными относительно точки О, если точки A, A", O лежат на одной прямой и OX = OX". Точка О считается симметричной сама себе (относительно О)

Две фигуры называются симметричными относительно точки О, если для каждой точки одной фигуры есть симметричная ей относительно точки О точка в другой фигуре и обратно

Как частный случай, фигура может быть симметрична сама себе относительно некоей точки О. Тогда эта точка О называется центром симметрии фигуры, а фигура центрально-симметричной

Определение

Центральной симметрией фигуры относительно О называется такое отображение этой фигуры, которое сопоставляет каждой ее точке точку, симметричную относительно О

Основное свойство: Центральная симметрия сохраняет расстояние, а направление изменяет на противоположное. Иначе говоря, любым двум точкам X и Y фигуры F соответствуют такие точки X" и Y", что X"Y" = -XY

Доказательство. Пусть при центральной симметрии с центром в точке О точки X и Y отобразились на X" и Y". Тогда, как ясно из определения центральной симметрии, OX" = -OX, OY" = -OY

Вместе с тем XY = OY - OX, X"Y" = OY" - OX"

Поэтому имеем: X"Y" = -OY + OX = -XY

Отсюда выходит, что центральная симметрия является движением, изменяющим направление на противоположное и наоборот, движение, изменяющее направление на противоположное, есть центральная симметрия

Центральная симметрия фигуры задается указанием одной пары существующих точек: если точка А отображается на А", то центр симметрии это середина отрезка AA"

Поворот вокруг прямой

Для более четкого представления о повороте вокруг прямой следует вспомнить поворот на плоскости около данной точки. Поворотом на плоскости около данной точки называется такое движение, при котором каждый луч, исходящий из данной точки, поворачивается на один и тот же угол в одном и том же направлении. Перейдем теперь к повороту в пространстве

Определение. Поворотом фигуры вокруг прямой a на угол (называется такое отображение, при котором в каждой плоскости, перпендикулярной прямой a, происходит поворот вокруг точки ее пересечения с прямой a на один и тот же угол (в одном и том же направлении. Прямая a называется осью поворота, а угол - углом поворота)

Отсюда видим, что поворот всегда задается осью, углом и направлением поворота

Теорема 1. Поворот вокруг прямой сохраняет расстояния, т.е. является движением

Теорема 2. Если движение пространства имеет множеством своих неподвижных точек прямую, то оно является поворотом вокруг этой прямой

Преобразования плоскости

или же любые последовательные p числа.

Данная система называется полною системою чисел, не сравнимых по модулю p или же полною системою вычетов по модулю p . Очевидно, что всякие p последовательных чисел образуют такую систему.

Все числа, принадлежащих к одному классу, имеют много общих свойств, следовательно по отношению к модулю их можно рассматривать как одно число. Каждое число, входящее в сравнение как слагаемое или множитель, может быть заменено, без нарушения сравнения, числом, сравнимым с ним, т.е. с числом, принадлежащим к одному и тому же классу.

Другой элемент, который является общим для всех чисел данного класса, является наибольший общий делитель каждого элемента этого класса и модуля p .

Пусть a и b сравнимы по модулю p , тогда

Теорема 1. Если в ax+b вместо x подставим последовательно все p членов полной системы чисел

Поэтому все числа ax+b , где x =1,2,...p -1 не сравнимы по модулю p (в противном случае, числа 1,2,...p -1 были бы сравнимы по модулю p .

Примечания

1) В данной статье под словом число будем понимать целое число.

Литература

• 1. К.Айрленд, М.Роузен. Классическое введение в современную теорию чисел.− М:Мир, 1987.
• 2. Г.Дэвенпорт. Высшая арифметика.− М:Наука, 1965.
• 3. П.Г. Лежен Дирихле. Лекции по теории чисел. − Москва, 1936.